Радианная мера угла

Радиан (рад) и градус (°) - это общепринятые единицы для измерения углов. Угол 1 рад чуть меньше угла 60°.

Слово "угол" употребляется в разных смыслах. В планиметрии под углом понимают часть плоскости, ограниченную двумя лучами, выходящими из одной точки. Вы наверняка помните смысл терминов "развернутый угол", "смежные углы", "прямой угол", "острый угол", "тупой угол", "полный угол" и сможете различить такие углы. Эти же понятия можно определить, измеряя углы, сравнивая их с некоторым эталоном. Если мы разделим полный угол на 360 равных частей, то получим угол, который принят за единицу при градусном измерении угла. По определению полный угол имеет меру 360°, развернутый -  180°, прямой - 90°, острый между 0° и 90°, тупой между 90° и 180°.

Следуя общей идее математики, мы хотим рассматривать и измерять не отдельно взятые, застывшие, а меняющиеся углы. Естественным процессом, порождающим различные углы, является вращательное движение.  

Возьмем два луча, исходящие иa одной точки О. Один луч считаем неподвижным, а другой будем вращать вокруг точки О.

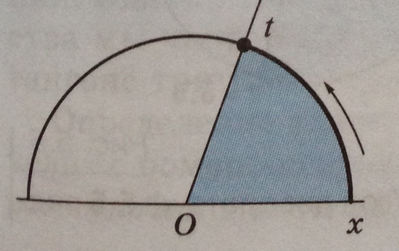
На плоскости есть два направления вращения, которым мы придадим противоположные знаки. По традиции вращение против хода часовой стрелки считается положительным, а противоположное ему - отрицательным.

Обозначим неподвижный луч Ox, a подвижный - Ot. Если мы остановим подвижный луч, то два луча разобьют плоскость на два геометрических угла. Одно и то же разбиение мы можем получить с помощью различных поворотов. Так как нас больше интересуют сами повороты, мы можем обобщить понятие угла, рассматривая "углы поворота" как некоторую характеристику вращательного движения.

Для того чтобы получить угол поворота на 1°, надо вращать  подвижный луч в положительном направлении от неподвижного до тех пор, пока он впервые не займет положение, образующее с неподвижным лучом геометрический угол 1°. Теперь с помощью этого "единичного поворота" мы сможем определить угол поворота на любое число градусов.

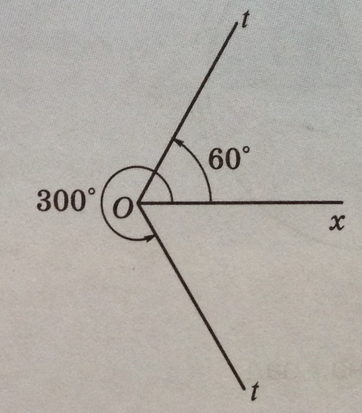
Это число может быть положительным или отрицательным - различать соответствующие углы поворота мы будем по направлению вращения. После поворота на 360° подвижный луч совместится с неподвижным, но мы можем продолжать вращение и считать, что можно рассматривать углы поворота на k градусов, где k - любое действительное число.

Для описания непрерывного вращения градусная мера поворота становится неудобной - с ней трудно связывать другие характеристики движения, например скорость, или соединять вращательное движение с иными движениями. Поэтому вводят другую меру угла поворота, так называемую радианную меру. 

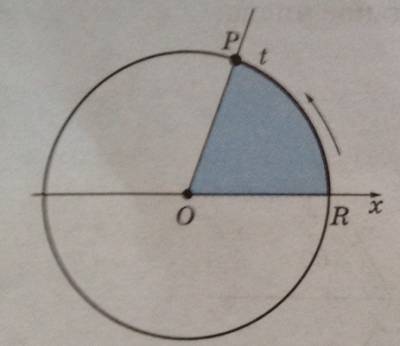
Опишем окружность радиусом R с центром в точке О. Начнем поворачивать подвижный луч и будем следить за точкой Р пересечения этого луча с окружностью.

При вращении подвижного луча от начального положения, совпадающего с неподвижным лучом, точка Р будет проходить по окружности некоторый путь, который можно измерить в тех же единицах длины, что и радиус R. Отношение пройденного пути к радиусу R не зависит радиуса. Если этому отношению еще приписать знак зависимости от направления вращения, то мы получим действительное число t, которое и называется радианной мерой угла поворота.

Так как число t является отношением двух однородных величин (длин), то оно безразмерно. Поэтому название меры - 1 рад - является в значительной мере условным. Можно говорить, что угол поворота равен 1 рад, но можно и просто сказать, что угол поворота равен единице.

Удобно выбрать значение радиуса R, равное 1. Окружность радиусом 1 с центром в точке О будем называть единичной окружностью. Тогда угол поворота численно будет равен пути, пройденному точкой Р по единичной окружности, со знаком, зависящим от направления вращения.

 

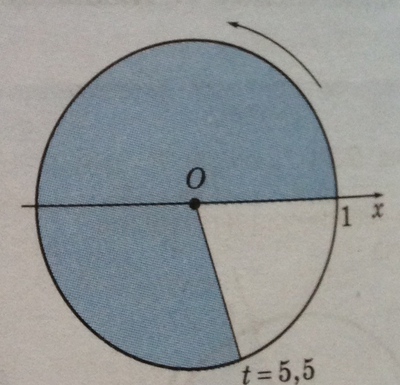
Так, пусть t - произвольное действительное число. Угол поворота на величину t (рад) - это такой угол поворота подвижного луча, при котором точка пересечения Р этого луча с единичной окружностью пройдет путь, равный ltl, причем направление вращения выбирается в зависимости от знака t.

Так как длина единичной окружности равна 2π = 6,283..., то поворот на угол π соответствует развернутому углу, на угол π/2 = 1,57 - прямому углу, а на угол 1 - углу, который в градусной мере приблизительно равен 57°.

Полезно запомнить, что часто встречающийся угол 60° чуть больше 1 рад: 60 ≈ 1,07 рад.